1. Startseite
  2. Science
  3. Scientific Highlights
  4. Current distribution in the quantum Hall regime: moving from the edge to the center

Current distribution in the quantum Hall regime: moving from the edge to the center

The lower panel shows the Hall resistance, RH, as a function of the magnetic field, B, as a red dashed line including the first plateau (ν = 1). The top panels show sketches of a section of a Hall bar sample including an inner contact (A). Thick black lines indicate the sample edges. The red (blue) hatches indicate a high (low) electrical potential due to the Hall effect if a current, I, is applied. For the case of a quantized Hall resistance, current flows only within specific regions (dark gray), which depend on the magnetic field. Local current contributions are indicated by magenta arrows. The current into the inner contact, IA(B), is plotted as a blue line. It is zero for the left (low B) side of the plateau, indicating that the inner contact is electrically separate from the current carrying regions (left sketch). However, current flows into the inner contact for the right side (larger B) of the plateau, indicating that the current carrying regions reach the inner contact (right sketch).

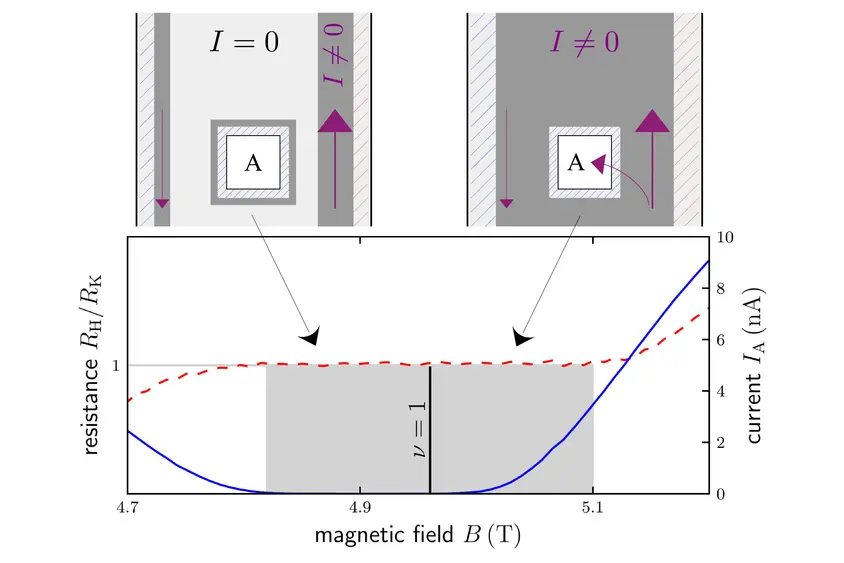
The quantum Hall effect (QHE) is one of the most remarkable phenomena in condensed matter physics. Its main features are quantized plateaus of the Hall resistance with fundamental, material-independent values RH=h/νe2, where e is the elementary charge and h the Planck constant. For the integer QHE, the plateaus are characterized by integer filling factors, ν=1,2,3,.... These plateaus can be directly measured and serve as today’s electrical resistance standard. The red dashed line in the figure shows a typical ν=1 plateau.

In text books, the QHE is still explained in terms of perfect one-dimensional edge channels, which carry a dissipationless current flowing chirally around an insulating bulk (Landauer-Büttiker picture [1]). More recently, it has been argued that this picture is incomplete, mainly because it neglects Coulomb interaction of the current-carrying electrons. Self-consistent calculations predict that the dissipationless current flows inside narrow channels along the sample edges near the left ends of the plateaus (low magnetic field), while it extends through the center (bulk) of the Hall bar sample near the right ends (high field) [2]. In the sketches, current-carrying regions (I≠0) are indicated by dark gray backgrounds and local contributions of the chiral current by magenta arrows.

In the reported experiment, we used an additional contact (labeled A in the sketches) placed in the center of the Hall bar, to detect the predicted bulk current. The blue line in the figure shows the current, IA, through this inner contact. We find IA=0 within the left half of the plateau indicating that contact A is isolated and the current flows along the edges. The onset of IA≠0 as the magnetic field is increased proves the existence of bulk current. To our knowledge, this is the first direct measurement of bulk current in the QHE. This result corresponds to the predictions of the self-consistent calculations and provides clear evidence for the importance of Coulomb interaction of the electrons in the integer QHE. It enables a better understanding of the current flow in the quantum Hall regime, which may facilitate the use of the QHE for quantum technology applications.

[1] M. Büttiker, “Absence of backscattering in the quantum Hall effect in multiprobe conductors,” Phys. Rev. B 38, 9375–9389 (1988).
[2] R. R. Gerhardts, “The effect of screening on current distribution and conductance quantization in narrow quantum Hall systems,” physica status solidi (b) 245, 378–392 (2008).

Title: Transition from edge- to bulk-currents in the quantum Hall regime
Authors: Sirt, S. and Umansky, V. Y. and Siddiki, A. and Ludwig, S.
Source: Appl. Phys. Lett., 126 (24): 243101, (2025).
DOI: 10.1063/5.0275599

Core Research Area (CReA): Nanoelectronics